
Introduction
From our earlier studies of UFO sightings, a recurring question has been the extent to which the frequency of sightings of inexplicable otherworldly phenomena depends on the population of an area. Intuitively: where there are more people to catch a glimpse of the unknown, there will be more reports of alien visitors.
Is this hypothesis, however, true? Do UFO sightings closely follow population or are there other, less comforting, factors at work?
In this short series of posts, we will build a statistical model of UFO sightings in the United States, based on data previously scraped from the National UFO Reporting Centre and see how well we can predict the rate of UFO sightings based on state population.
This series of posts is part tutorial and part exploration of a set of modelling tools and techniques. Specifically, we will use Generalized Linear Models (GLMs), Bayesian inference, and the Stan probabilistic programming language to unveil the relationship between unsuspecting populations of US states and the dread sightings of extraterrestrial truth that they experience.
Data
As mentioned, we will rely on data from NUFORC for extraterrestrial sightings.
For population data, we can rely on the the FRED database for historical US state-level census data. The combination of these datasets provides us with a count of UFO sightings per year for each state, and the population of that state in that year.
The downloading and scraping code is included here:
For ease, we will treat each year’s count of sightings as independent from the previous year’s — we do not make an assumption that the number of sightings in each year is based on the number of sightings in the previous year, but is rather due to the unknowable schemes of alien minds. (If extraterrestrials visitors were colonising areas in secrecy rather than making sporadic visits, and thus being seen repeatedly, we might not want to make such a bold assumption.) Each annual count will be treated as an individual, independent data point relating population to count, with each observation tagged by state.
For simplicity, particularly in building later models, we will restrict ourselves to sightings post 1990, roughly reflecting a period in which the NUFORC data sees a significant increase in reporting and thus relies less on historical reports. (NUFORC’s phone hotline has existed since 1974, and its web form since 1998.)
An Awful Simplicity
To begin, we start with the most basic form of model: a simple linear relationship between the count of sightings and the population of the state at that time. If sightings were purely dependent on population, it might be reasonable to assume that such a model would fit the data fairly well.
This relationship can be plotted with relative ease using the geom_smooth() function of ggplot2 in R. For opening our eyes to the awful truth contained in the data, this is a useful first step.
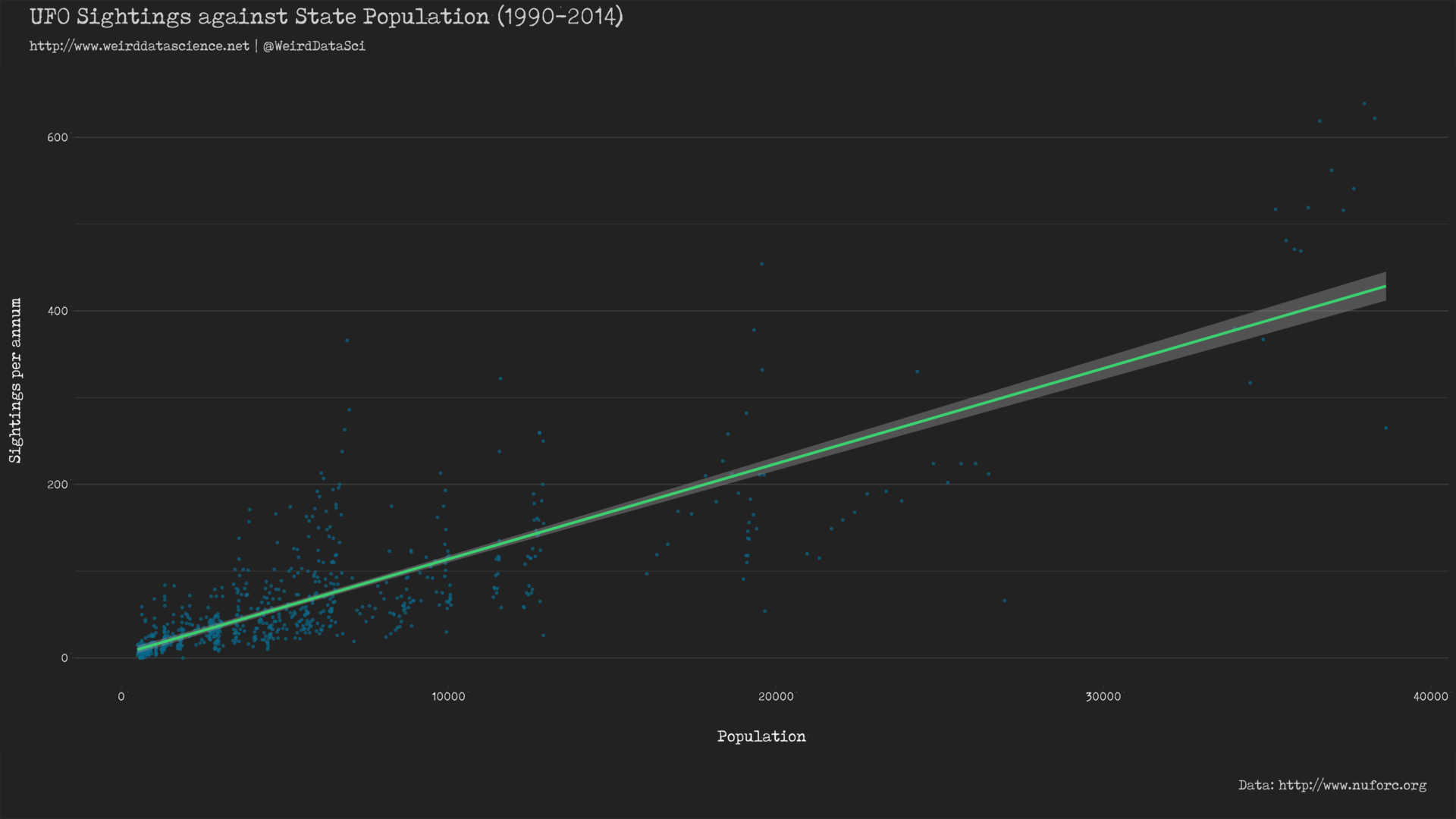
While this graph does seem to support the argument that sightings increase with population in general, a closer inspection shows that the individual data points are clearly clustered. If we highlight the location of each data point, colouring points by US state, this becomes clearer:
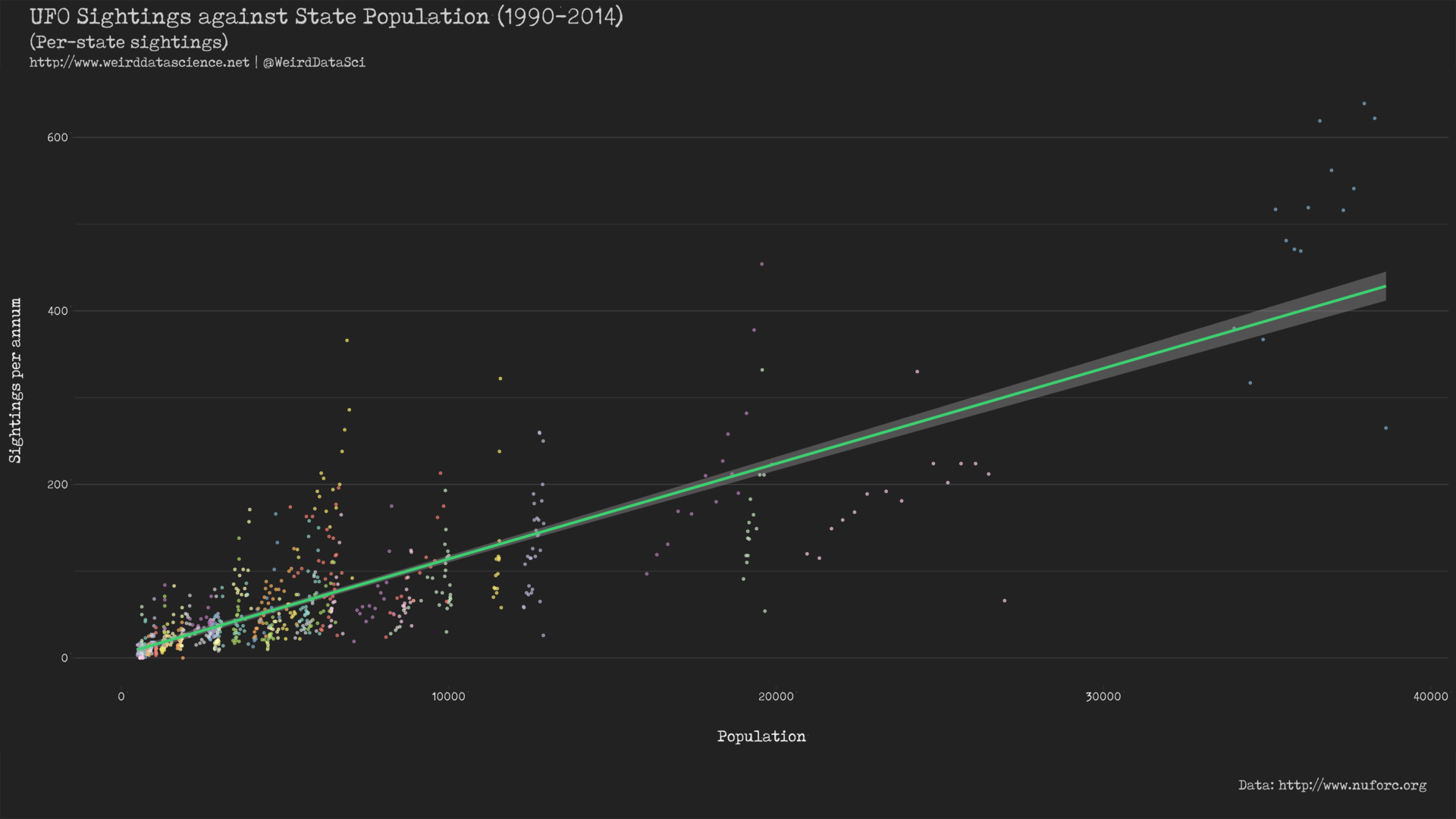
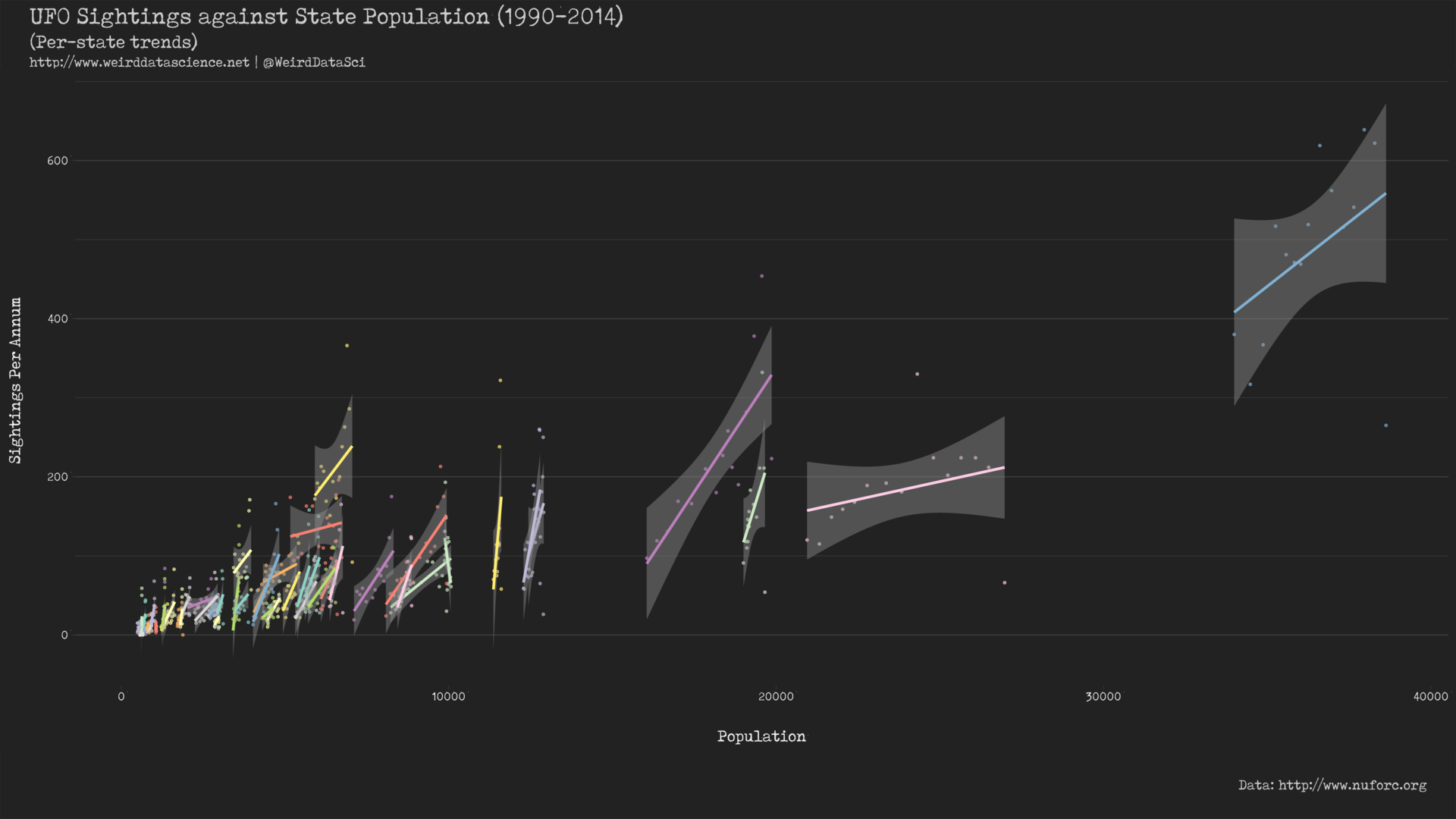
This strongly suggests that, in preference to the simple linear model across all sightings, we might instead fit a linear model individually to each state:
The code to produce the above graphs from the NUFORC and FRED data is given below:
Result
The plots shown here strongly indicate that the rate of dread interplanetary visitations per capita varies differently per state. It seems, therefore, that while the number of sightings is generally proportional to population, the specific relationship is state-dependent.
This simple linear model is, however, entirely unsatisfactory in describing the data, despite its support for the argument that different states have different underlying rates of sightings.
In the next post, therefore, we will delve deeper into the unsettling relationships between UFO sightings and the innocent humans to which they are drawn. To do so, we will have to consider a class of techniques that go beyond the normal distribution that underpins key assumptions of the simple linear models used here, and so move into the eldritch world of generalized linear models.

Great work. The shell script doesn’t work for me. I’m wondering whether you can share the data in a github repo. Thanks in advance.
I really should put all this code up in github. I’ve been a little wary of sharing datasets like the scraped NUFORC one as they’re all from other people and projects, but given that all of this is public I think it should be reasonable to share CSVs to allow reproducability. I’ll look into it very soon!